3) Considerando os requisitos do sistema (24 V e 10 A), seria possível atender essas condições com dois geradores e com essas duas configurações? Se não, proponha uma associação alternativa (série-paralelo) que permita atender à demanda, justificando com cálculos. 
ATIVIDADE 2 – MAT – ANÁLISE MATEMÁTICA – 53_2025
ATIVIDADE 2 – MAT – ANÁLISE MATEMÁTICA – 53_2025
DESTCH, Denise Trevisoli. CRAVEIRO, Irene Magalhães. KATO, Lilian Akemi. SCHULZ, Rodrigo André. RUIZ, Simone Francisco. Análise Matemática. Maringá: Unicesumar, 2020. Adaptado.
Com apoio do texto base, analise as asserções a seguir.
I – A série a seguir é convergente
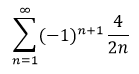
PORQUE
II – As condições do critério de Leibniz são satisfeitas, tomando an= 1/n.
Assinale a alternativa que apresenta corretamente a relação entre elas.
As asserções I e II são verdadeiras, e a asserção II é uma justificativa correta para I.
As asserções I e II são verdadeiras, mas a asserção II não é uma justificativa correta para I.
A asserção I é verdadeira e a asserção II é falsa
A asserção I é falsa e a asserção II é verdadeira
As asserções I e iI são falsas.
DESTCH, Denise Trevisoli. CRAVEIRO, Irene Magalhães. KATO, Lilian Akemi. SCHULZ, Rodrigo André. RUIZ, Simone Francisco. Análise Matemática. Maringá: Unicesumar, 2020.
Em vista do texto acima, assinale a alternativa que apresenta corretamente a relação entre as asserções abaixo.
I – Para todo n ∈ N a soma dos números 1+3+5+7+⋯+(2n-1)+⋯ =n2
PORQUE
II – Definido P(n)=1+3+5+7+⋯+2n-1+⋯ =n2, tem-se que P(1) é verdadeiro, pois 1=12.
As asserções I e II são verdadeiras e a asserção II é uma justificativa correta para I.
As asserções I e II são verdadeiras, mas a asserção II não é uma justificativa correta para I.
A asserção I é verdadeira e a asserção II é falsa.
A asserção I é falsa e a asserção II é verdadeira.
As asserções I e II são falsas.
Considerando os conjuntos A = {1, 2, 3} e B = {3, 4, 7, 8}, e a função f: A→B, tal que f(1) = 3, f(2) = 7 e f(3) = 8, avalie as afirmativas a seguir.
I – f é uma função injetora.
II – f é uma função sobrejetora.
III – f é uma função bijetora.
É correto o que se afirma em:
I, apenas.
III, apenas.
I e II, apenas.
II e III, apenas.
I, II e III.
É correto o que se afirma em:
I e II, apenas.
I e IV, apenas.
II e IV, apenas.
I, II e IV, apenas.
I, II, III e IV.
Sejam X=(0,2) e Y=[-3,3], ambos intervalos definidos na reta real.
Fonte: Elaborado pelo professor, 2024.
Sabendo disso, avalie as afirmativas a seguir:
I. X ∩ Y é um conjunto aberto.
II. X é um intervalo fechado e Y é enumerável.
III. X ∪ Y é um conjunto compacto.
IV. X é um conjunto limitado.
É correto o que se afirma em:
I e II, apenas.
I e III, apenas.
I e IV, apenas.
I, III e IV, apenas.
I, II, III e IV.
A respeito dessas asserções, assinale a alternativa correta:
As asserções I e II são verdadeiras e a II é uma justificativa correta da I.
As asserções I e II são verdadeiras, mas a II não é uma justificativa correta da I.
A asserção I é uma proposição verdadeira e a II é uma proposição falsa.
A asserção I é uma proposição falsa e a II é uma proposição verdadeira.
As asserções I e II são falsas.
A respeito dessas asserções, assinale a alternativa correta:
As asserções I e II são verdadeiras, e a II é uma justificativa correta da I.
As asserções I e II são verdadeiras, mas a II não é uma justificativa correta da I.
A asserção I é uma proposição verdadeira e a II é uma proposição falsa.
A asserção I é uma proposição falsa e a II é uma proposição verdadeira.
As asserções I e II são falsas.
Sabendo disso, avalie as seguintes afirmativas:
I. O conjunto Y tem supremo, mas não tem máximo.
II. Os conjuntos X e Y são compactos.
III. Todo máximo é supremo, mas nem todo supremo é máximo.
IV. Todo ínfimo é cota inferior, mas nem toda cota inferior é ínfimo.
É correto o que se afirma em:
I e III, apenas.
I e IV, apenas.
I, II e III, apenas.
I, III e IV, apenas.
I, II, III e IV.
DESTCH, Denise Trevisoli. CRAVEIRO, Irene Magalhães. KATO, Lilian Akemi. SCHULZ, Rodrigo André. RUIZ, Simone Francisco. Análise Matemática. Maringá: Unicesumar, 2020. Adaptado.
Em vista do texto acima, analise as séries a seguir.
I –
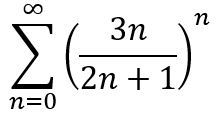
II –
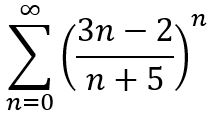
III –
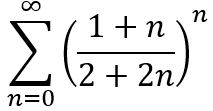
O(s) item(ns) que apresenta(m) série(s) convergente(s) pelo teste da raiz são:
I apenas.
III, apenas.
I e II, apenas.
II e III, apenas.
I, II e III.
SILVA, Marcos Noé Pedro da. \”Tipos de Função\”; Brasil Escola. Disponível em: https://brasilescola.uol.com.br/matematica/tipos-de-funcao.htm. Acesso em 28 de julho de 2022.
Com apoio do texto base, analise as afirmações a seguir.
Considere as funções abaixo definidas nos números Reais, isto é, f: R→R .
I – f(x)=x+2 é uma função injetora.
II – f(x)=x^2 é uma função injetora.
III – f(x)=√x é uma função sobrejetora.
IV – f(x)=x^4+10 é uma função bijetora.
É correto o que se diz em:
I, apenas.
III, apenas.
I e II, apenas.
II, III e IV, apenas.
I, II, III e IV.
Olá, somos a Prime Educacional!
Nossa equipe é composta por profissionais especializados em diversas áreas, o que nos permite oferecer uma assessoria completa na elaboração de uma ampla variedade de atividades. Estamos empenhados em garantir a autenticidade e originalidade de todos os trabalhos que realizamos.
Ficaríamos muito satisfeitos em poder ajudar você. Entre em contato conosco para solicitar o seu serviço.
Produtos relacionados
