ATIVIDADE 3 – MAT – ANÁLISE MATEMÁTICA – 53_2025
ATIVIDADE 3 – MAT – ANÁLISE MATEMÁTICA – 53_2025
I. Uma sequência (an) é convergente se os termos an forem sempre positivos.
II. Se uma sequência é convergente, então ela é também monótona.
III. A definição de sequência convergente implica que a sequência é limitada.
É correto o que se afirma em:
I, apenas.
III, apenas.
I e II, apenas.
I e III, apenas.
I, II e III.
Uma função é contínua num intervalo , se, e somente se, f for contínua em todos os pontos do intervalo.
DESTCH, Denise Trevisoli. CRAVEIRO, Irene Magalhães. KATO, Lilian Akemi. SCHULZ, Rodrigo André. RUIZ, Simone Francisco. Análise Matemática. Maringá: Unicesumar, 2020. Adaptado.
Em vista do texto acima, assinale a alternativa que apresenta corretamente a relação entre as asserções abaixo.
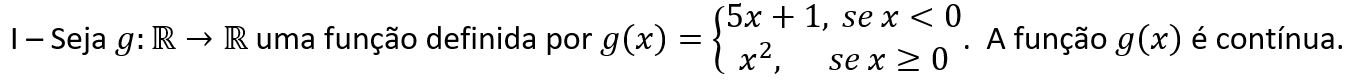
PORQUE
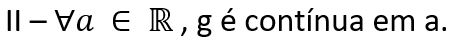
As asserções I e II são verdadeiras e a asserção II é uma justificativa correta para a asserção I.
As asserções I e II são verdadeiras, mas a asserção II não é uma justificativa correta para a asserção I.
A asserção I é verdadeira e a asserção II é falsa.
A asserção I é falsa e a asserção II é verdadeira.
As asserções I e II são falsas.
I – A função f(x) = |x| é contínua e derivável em todos os pontos
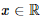.PORQUE
II – A função não é derivável em x = 0. Uma maneira de mostrar e verificar, através dos limites laterais da definição de derivada, que eles são diferentes, então não existe a derivada:
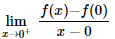
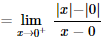
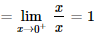
e
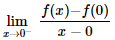
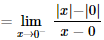
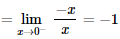
As asserções I e II são proposições verdadeiras e a II é uma justificativa da I.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.
A asserção I é uma proposição verdadeira e a II é uma proposição falsa.
A asserção I é uma proposição falsa e a II é uma proposição verdadeira.
As asserções I e II são proposições falsas.
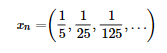
Analise as afirmações a seguir.
I – A sequência xn possui termo igual a
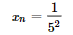.II – A sequência xn é monótona decrescente.
III – A série
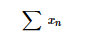, formada pelos termos da sequência dada, é divergente.IV – A série
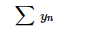, cujo termo geral é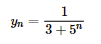
é convergente.
É correto o que se diz em.
I e II, apenas.
I e III, apenas.
II e IV, apenas.
I, II e IV, apenas.
I, II, III e IV.
DESTCH, Denise Trevisoli. CRAVEIRO, Irene Magalhães. KATO, Lilian Akemi. SCHULZ, Rodrigo André. RUIZ, Simone Francisco. Análise Matemática. Maringá: Unicesumar, 2020. Adaptado.
Com base no texto acima, considere 4 e 7 elementos do conjunto dos números reais. Analise as afirmativas a seguir:
I – 4+7 = 7+4
II – 4⋅7 = 7⋅4
As afirmativas I e II estão relacionadas a:
Propriedade Lógica
Propriedade Comutativa
Propriedade Associativa
Propriedade Demonstrativa
Propriedade de Soma e Produto
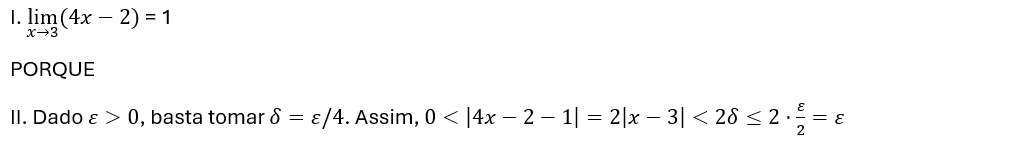
A respeito dessas asserções, assinale a alternativa correta:
As asserções I e II são verdadeiras, e a II é uma justificativa correta da I.
As asserções I e II são verdadeiras, mas a II não é uma justificativa correta da I.
A asserção I é uma proposição verdadeira e a II é uma proposição falsa.
A asserção I é uma proposição falsa e a II é uma proposição verdadeira.
As asserções I e II são falsas.
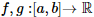funções integráveis, avalie as afirmações a seguir.
I –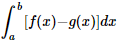 
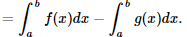
II – Se a < 0 e b = 1, então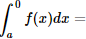 
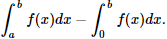
III – Se a = b e f(x) = 3, para todo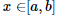 
, então 
.
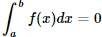IV – Se f(x) < 0 e g(x) > 0, para todo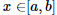 
, então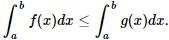 
É correto o que se afirma em:
I, apenas.
II e IV, apenas.
III e IV, apenas.
I, II e III, apenas.
I, II, III e IV.
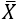.Elaborado pelo professor, 2024.
Considerando os conjuntos A=(1,4) e B=(4,7), avalie as afirmativas a seguir:
É correto o que se afirma em:
I, apenas.
III, apenas.
I e II, apenas.
I e III, apenas.
I, II e III.
Leibniz foi um gênio universal. Sua obra toca praticamente todos os campos do conhecimento. Em paralelo a Newton, os dois contribuíram de forma significativa para o desenvolvimento dos conceitos que hoje temos presente no Cálculo Diferencial. Entretanto, o conceito de integral começou a ser construído muito antes das contribuições desses dois grandes matemáticos. As primeiras noções sobre o conceito de integral aparecem nos trabalhos de Arquimedes (287-212 a.C.) referentes a área de figuras planas.
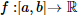integrável, 
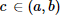e P partição de [a,b]. A respeito das propriedades de integação dessa função, avalie as afirmativas a seguir.
I – A função f é integrável em [a,c] e [c,b].
II –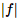 
é integrável e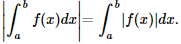 
III –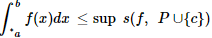 
e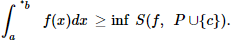 
IV – Se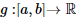 
é integrável e 
para todo 
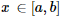, então, 
.
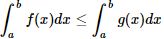É correto o que se afirma em:
I e IV, apenas.
I e III, apenas.
II e IV, apenas.
I, II e IV, apenas.
II, III e IV, apenas.
Considere a função contínua f(x)=x³-3x+1 definida no intervalo [0,1].
Fonte: Elaborado pelo professor, 2024.
Utilize o Teorema do Valor Intermediário, e avalie as afirmativas a seguir.
I. Existe um ponto c em (0,1) tal que f(c)=0.
II. O Teorema do Valor Intermediário garante que a função atinge o valor f(x)=1 em pelo menos um ponto do intervalo [0,1].
III. É possível determinar a existência de c tal que f(c)=0 apenas com base no TVI.
IV. Para algum valor L entre f(0) e f(1), a função f(x) atinge f(c)=L para pelo menos um c em [0,1].
É correto o que se afirma em:
I e III, apenas.
I e IV, apenas.
I, II e IV, apenas.
I, III e IV, apenas.
I, II, III e IV.
Olá, somos a Prime Educacional!
Nossa equipe é composta por profissionais especializados em diversas áreas, o que nos permite oferecer uma assessoria completa na elaboração de uma ampla variedade de atividades. Estamos empenhados em garantir a autenticidade e originalidade de todos os trabalhos que realizamos.
Ficaríamos muito satisfeitos em poder ajudar você. Entre em contato conosco para solicitar o seu serviço.
Produtos relacionados
