Sobre as funções contínuas e deriváveis em um ponto, analise as afirmações a seguir e assinale a alternativa correta.
I – A função f(x) = |x| é contínua e derivável em todos os pontos
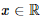.PORQUE
II – A função não é derivável em x = 0. Uma maneira de mostrar e verificar, através dos limites laterais da definição de derivada, que eles são diferentes, então não existe a derivada:
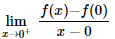
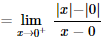
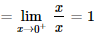
e
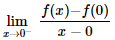
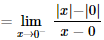
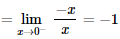
As asserções I e II são proposições verdadeiras e a II é uma justificativa da I.
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.
A asserção I é uma proposição verdadeira e a II é uma proposição falsa.
A asserção I é uma proposição falsa e a II é uma proposição verdadeira.
As asserções I e II são proposições falsas.
Olá, somos a Prime Educacional!
Nossa equipe é composta por profissionais especializados em diversas áreas, o que nos permite oferecer uma assessoria completa na elaboração de uma ampla variedade de atividades. Estamos empenhados em garantir a autenticidade e originalidade de todos os trabalhos que realizamos.
Ficaríamos muito satisfeitos em poder ajudar você. Entre em contato conosco para solicitar o seu serviço.
Produtos relacionados
